谈一下"求线段交点"的几种算法(js实现,完整版)
日期:2014-05-16 浏览次数:20704 次
谈谈"求线段交点"的几种算法(js实现,完整版)
谈谈"求线段交点"的几种算法(js实现,完整版)
"求线段交点"是一种非常基础的几何计算, 在很多游戏中都会被使用到.
下面我就现学现卖的把最近才学会的一些"求线段交点"的算法说一说, 希望对大家有所帮助.
本文讲的内容都很初级, 主要是面向和我一样的初学者, 所以请各位算法帝们轻拍啊 嘎嘎
===============================
算法一: 求两条线段所在直线的交点, 再判断交点是否在两条线段上.
求直线交点时 我们可通过直线的一般方程 ax+by+c=0 求得(方程中的abc为系数,不是前面提到的端点,另外也可用点斜式方程和斜截式方程,此处暂且不论).
然后根据交点的与线段端点的位置关系来判断交点是否在线段上. 公式如下图:

实现代码如下 :
算法一思路比较清晰易懂, 但是性能并不高. 因为它在不确定交点是否有效(在线段上)之前, 就先去计算了交点, 耗费了较多的时间.
如果最后发现交点无效, 那么之前的计算就白折腾了. 而且整个计算的过程也很复杂.
那么有没有一种思路,可以让我们先判断是否存在有效交点,然后再去计算它呢?
显然答案是肯定的. 于是就有了后面的一些算法.
===============================
算法二: 判断每一条线段的两个端点是否都在另一条线段的两侧, 是则求出两条线段所在直线的交点, 否则不相交.
第一步判断两个点是否在某条线段的两侧, 通常可采用投影法:
求出线段的法线向量, 然后把点投影到法线上, 最后根据投影的位置来判断点和线段的关系. 见下图
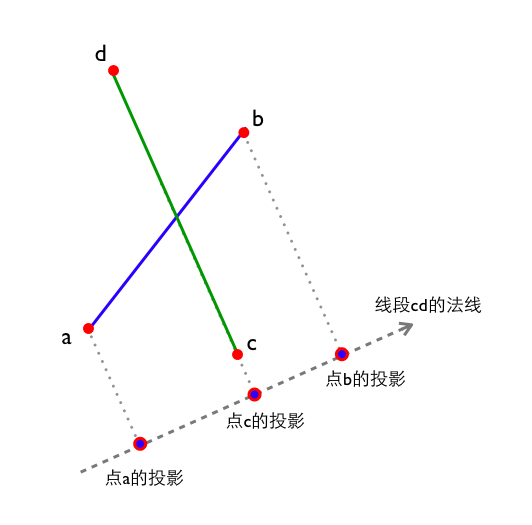
点a和点b在线段cd法线上的投影如图所示, 这时候我们还要做一次线段cd在自己法线上的投影(选择点c或点d中的一个即可).
主要用来做参考.
图中点a投影和点b投影在点c投影的两侧, 说明线段ab的端点在线段cd的两侧.
同理, 再判断一次cd是否在线段ab两侧即可.
求法线 , 求投影 什么的听起来很复杂的样子, 实际上对于我来说也确实挺复杂,在几个月前我也不会(念书那会儿的几何知识都忘光了 :'( )'
不过好在学习和实现起来还不算复杂, 皆有公式可循:
求线段ab的法线:
注意: 其中 normalLine.x和normalLine.y的几何意义表示法线的方向, 而不是坐标.
求点c在法线上的投影位置:
注意: 这里的"投影位置"是一个标量, 表示的是到法线原点的距离, 而不是投影点的坐标.
通常知道这个距离就足够了.
当我们把图中 点a投影(distA),点b投影(distB),点c投影(distC) 都求出来之后, 就可以很容易的根据各自的大小判断出相对位置.
distA==distB==distC 时, 两条线段共线
distA==distB!=distC 时, 两条线段平行
distA 和 distB 在distC 同侧时, 两条线段不相交.
distA 和 distB 在distC 异侧时, 两条线段是否相交需要再判断点c点d与线段ab的关系.
前面的那些步骤, 只是实现了"判断线段是否相交", 当结果为true时, 我们还需要进一步求交点.
求交点的过程后面再说, 先看一下该算法的完整实现 :
谈谈"求线段交点"的几种算法(js实现,完整版)
"求线段交点"是一种非常基础的几何计算, 在很多游戏中都会被使用到.
下面我就现学现卖的把最近才学会的一些"求线段交点"的算法说一说, 希望对大家有所帮助.
本文讲的内容都很初级, 主要是面向和我一样的初学者, 所以请各位算法帝们轻拍啊 嘎嘎
引用
已知线段1(a,b) 和线段2(c,d) ,其中a b c d为端点, 求线段交点p .(平行或共线视作不相交)
===============================
算法一: 求两条线段所在直线的交点, 再判断交点是否在两条线段上.
求直线交点时 我们可通过直线的一般方程 ax+by+c=0 求得(方程中的abc为系数,不是前面提到的端点,另外也可用点斜式方程和斜截式方程,此处暂且不论).
然后根据交点的与线段端点的位置关系来判断交点是否在线段上. 公式如下图:

实现代码如下 :
function segmentsIntr(a, b, c, d){
/** 1 解线性方程组, 求线段交点. **/
// 如果分母为0 则平行或共线, 不相交
var denominator = (b.y - a.y)*(d.x - c.x) - (a.x - b.x)*(c.y - d.y);
if (denominator==0) {
return false;
}
// 线段所在直线的交点坐标 (x , y)
var x = ( (b.x - a.x) * (d.x - c.x) * (c.y - a.y)
+ (b.y - a.y) * (d.x - c.x) * a.x
- (d.y - c.y) * (b.x - a.x) * c.x ) / denominator ;
var y = -( (b.y - a.y) * (d.y - c.y) * (c.x - a.x)
+ (b.x - a.x) * (d.y - c.y) * a.y
- (d.x - c.x) * (b.y - a.y) * c.y ) / denominator;
/** 2 判断交点是否在两条线段上 **/
if (
// 交点在线段1上
(x - a.x) * (x - b.x) <= 0 && (y - a.y) * (y - b.y) <= 0
// 且交点也在线段2上
&& (x - c.x) * (x - d.x) <= 0 && (y - c.y) * (y - d.y) <= 0
){
// 返回交点p
return {
x : x,
y : y
}
}
//否则不相交
return false
}
算法一思路比较清晰易懂, 但是性能并不高. 因为它在不确定交点是否有效(在线段上)之前, 就先去计算了交点, 耗费了较多的时间.
如果最后发现交点无效, 那么之前的计算就白折腾了. 而且整个计算的过程也很复杂.
那么有没有一种思路,可以让我们先判断是否存在有效交点,然后再去计算它呢?
显然答案是肯定的. 于是就有了后面的一些算法.
===============================
算法二: 判断每一条线段的两个端点是否都在另一条线段的两侧, 是则求出两条线段所在直线的交点, 否则不相交.
第一步判断两个点是否在某条线段的两侧, 通常可采用投影法:
求出线段的法线向量, 然后把点投影到法线上, 最后根据投影的位置来判断点和线段的关系. 见下图

点a和点b在线段cd法线上的投影如图所示, 这时候我们还要做一次线段cd在自己法线上的投影(选择点c或点d中的一个即可).
主要用来做参考.
图中点a投影和点b投影在点c投影的两侧, 说明线段ab的端点在线段cd的两侧.
同理, 再判断一次cd是否在线段ab两侧即可.
求法线 , 求投影 什么的听起来很复杂的样子, 实际上对于我来说也确实挺复杂,在几个月前我也不会(念书那会儿的几何知识都忘光了 :'( )'
不过好在学习和实现起来还不算复杂, 皆有公式可循:
求线段ab的法线:
var nx=b.y - a.y,
ny=a.x - b.x;
var normalLine = { x: nx, y: ny };
注意: 其中 normalLine.x和normalLine.y的几何意义表示法线的方向, 而不是坐标.
求点c在法线上的投影位置:
var dist= normalLine.x*c.x + normalLine.y*c.y;
注意: 这里的"投影位置"是一个标量, 表示的是到法线原点的距离, 而不是投影点的坐标.
通常知道这个距离就足够了.
当我们把图中 点a投影(distA),点b投影(distB),点c投影(distC) 都求出来之后, 就可以很容易的根据各自的大小判断出相对位置.
distA==distB==distC 时, 两条线段共线
distA==distB!=distC 时, 两条线段平行
distA 和 distB 在distC 同侧时, 两条线段不相交.
distA 和 distB 在distC 异侧时, 两条线段是否相交需要再判断点c点d与线段ab的关系.
前面的那些步骤, 只是实现了"判断线段是否相交", 当结果为true时, 我们还需要进一步求交点.
求交点的过程后面再说, 先看一下该算法的完整实现 :
function segmentsIntr(a, b, c, d){
//线段ab的法线N1
var nx1 = (b.y - a.y), ny1 = (a.x - b.x);
//线段cd的法线N2
var nx2 = (d.y - c.y), ny2 = (c.x - d.x);
//两条法线做叉乘, 如果结果为0, 说明线段ab和线段cd平行或共线,不相交
var denominator = nx1*ny2 - ny1*nx2;
if (denominator==0) {
return false;
}
//在法线N2上的投影
var distC_N2=nx2 * c.x + ny2 * c.y;
var distA_N2=nx2 * a.x + ny2 * a.y
免责声明: 本文仅代表作者个人观点,与爱易网无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
